How to build and evaluate models using Microsoft R Server?
This blog post is continuation my earlier post where we performed data cleaning and feature engineering on the Kaggle data set. We also studied the relationship between the label (gender in this case) and other covariates.
Overview
In this post we will start of from where we left and play around with various machine learning functions from the powerful RevoScaleR package. Just to refresh the memory lets quickly take a look at our data set.
allfeatnew.xdf <- "allfeatnew.xdf"
# Convert gender to numeric binary values
allfeatnew.xdf <- rxDataStep(allfeatnew.xdf, allfeatnew.xdf,
transforms = list(
bin_gender = as.numeric(gender) - 1
),
overwrite = TRUE)
i <- rxGetInfo(allfeatnew.xdf, getVarInfo = TRUE, numRows = 5)
i$varInfo
## Var 1: gender
## 2 factor levels: F M
## Var 2: age, Type: integer, Low/High: (11, 89)
## Var 3: new_id, Type: integer, Low/High: (3, 74645)
## Var 4: med_lon, Type: numeric, Low/High: (-169.4634, 136.1350)
## Var 5: med_lat, Type: numeric, Low/High: (-20.3239, 50.2403)
## Var 6: num_apps, Type: numeric, Low/High: (1.0000, 48132.0000)
## Var 7: day
## 7 factor levels: Su M Tu W Th F Sa
## Var 8: hr
## 24 factor levels: 0 1 2 3 4 ... 19 20 21 22 23
## Var 9: bin_gender, Type: numeric, Low/High: (0.0000, 1.0000)
There are 8 variables in total. Please note that we will be treating the
gender, day and hr variable as factors. Our objective is to
predict the gender based on the other variables. Here are top few rows
of the dataset.
i$data
## gender age new_id med_lon med_lat num_apps day hr bin_gender
## 1 M 35 3 0.00000 0.00000 53 Su 14 1
## 2 F 37 12 76.76741 20.38272 81 W 14 0
## 3 M 32 14 0.00000 0.00000 154 Th 22 1
## 4 F 28 16 120.25431 31.89642 109 Su 12 0
## 5 M 75 19 117.23261 39.12894 303 F 17 1
Model Building
Clearly this is the case of a two-class classification. We will build 3 different models to evaluate the performance and choose the best performing model.
Before we get started lets split our data in to train and test data sets
using the rxSplit function.
set.seed(123)
train.test.xdf <- rxSplit(inData = allfeatnew.xdf,
splitByFactor="newVar",
transforms = list(
newVar = factor(
sample(0:1, size=.rxNumRows,
replace=TRUE,
prob=c(.10, .9)),
levels=0:1,
labels = c("Test", "Train")
)
),
overwrite = TRUE)
Two xdf files will be created in the source folder. Lets quickly check
the proportion of gender labels in both the files
library(dplyr)
s <- rxSummary(~gender, data = train.test.xdf[[1]])
s$categorical[[1]] %>% mutate(Counts = round(Counts/sum(Counts), 2))
## gender Counts
## 1 F 0.33
## 2 M 0.67
s <- rxSummary(~gender, data = train.test.xdf[[2]])
s$categorical[[1]] %>% mutate(Counts = round(Counts/sum(Counts), 2))
## gender Counts
## 1 F 0.35
## 2 M 0.65
The lables pretty much event distributed in both train and test data sets so we can proceed.
Logistic Regression
Lets start with the stepwise logistic regression. This helps us to automatically choose the best variables to be included in the model.
logit_model <- rxLogit(gender ~ age, data = train.test.xdf[[2]],
variableSelection = rxStepControl(
method = "stepwise",
scope = ~ age + med_lon + med_lat +
num_apps + day + hr
))
s <- summary(logit_model)
s$coefficients
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.7492060637 9.887565e-02 7.5772558 2.220446e-16
## age -0.0065237287 1.481153e-03 -4.4044936 1.060313e-05
## med_lon 0.0127986987 1.385970e-03 9.2344713 2.220446e-16
## num_apps 0.0001775175 1.998731e-05 8.8815101 2.220446e-16
## hr=0 0.2266011550 1.024686e-01 2.2114196 2.700679e-02
## hr=1 0.3319440297 1.349068e-01 2.4605439 1.387266e-02
## hr=2 0.1779511417 1.538579e-01 1.1565943 2.474381e-01
## hr=3 0.4766070671 1.829298e-01 2.6054090 9.176463e-03
## hr=4 0.2315232074 1.803135e-01 1.2840036 1.991407e-01
## hr=5 -0.1856216514 1.271494e-01 -1.4598708 1.443256e-01
## hr=6 -0.1112880688 1.056986e-01 -1.0528810 2.923955e-01
## hr=7 -0.2628934990 1.023690e-01 -2.5680960 1.022588e-02
## hr=8 -0.1239000548 1.033472e-01 -1.1988718 2.305778e-01
## hr=9 -0.2235041217 1.041353e-01 -2.1462864 3.185013e-02
## hr=10 -0.2015555531 1.040060e-01 -1.9379216 5.263279e-02
## hr=11 -0.1692954778 1.086031e-01 -1.5588455 1.190329e-01
## hr=12 -0.1274890580 1.088477e-01 -1.1712613 2.414938e-01
## hr=13 -0.2753561016 1.121173e-01 -2.4559643 1.405071e-02
## hr=14 -0.1377214530 1.143229e-01 -1.2046708 2.283304e-01
## hr=15 -0.1878044894 1.169417e-01 -1.6059672 1.082811e-01
## hr=16 -0.1487536243 1.165967e-01 -1.2757966 2.020274e-01
## hr=17 -0.1404790253 1.171812e-01 -1.1988186 2.305985e-01
## hr=18 -0.0530219908 1.176963e-01 -0.4504982 6.523513e-01
## hr=19 -0.1146612795 1.147277e-01 -0.9994214 3.175906e-01
## hr=20 -0.2684656639 1.107639e-01 -2.4237648 1.536055e-02
## hr=21 -0.3370245661 1.097665e-01 -3.0703778 2.137881e-03
## hr=22 -0.1779859250 1.135485e-01 -1.5674882 1.170006e-01
## hr=23 NA NA NA NA
## med_lat -0.0333165225 4.822961e-03 -6.9078975 4.918954e-12
As we can see from the above coefficients, the day variable is dropped
along with hr=23. This is consistant with the results of the
statistical test we performed between gender and day in the earlier
post.
Decision Forest
Lets build a decision forest model with the training data.
forest_model <- rxDForest(formula = gender ~ age + med_lon + med_lat +
num_apps + day + hr,
data = train.test.xdf[[2]],
outFile = "forest.xdf",
method = "class",
maxDepth = 5,
nTree = 50,
mTry = 2,
seed = 123,
overwrite = TRUE)
forest_model
##
## Call:
## rxDForest(formula = gender ~ age + med_lon + med_lat + num_apps +
## day + hr, data = train.test.xdf[[2]], outFile = "forest.xdf",
## overwrite = TRUE, method = "class", maxDepth = 5, nTree = 50,
## mTry = 2, seed = 123)
##
##
## Type of decision forest: class
## Number of trees: 50
## No. of variables tried at each split: 2
##
## OOB estimate of error rate: 34.72%
## Confusion matrix:
## Predicted
## gender F M class.error
## F 5 7316 0.9993170332
## M 7 13765 0.0005082777
Gradient Boosted Decision Tree
Finally, we will build a gradient bossted decision tree model.
btree_model <- rxBTrees(formula = gender ~ age + med_lon + med_lat +
num_apps + day + hr,
data = train.test.xdf[[2]],
outFile = "btree.xdf",
cp=0.01,
nTree=50,
mTry=3,
lossFunction="bernoulli",
seed = 123,
overwrite = TRUE)
btree_model
##
## Call:
## rxBTrees(formula = gender ~ age + med_lon + med_lat + num_apps +
## day + hr, data = train.test.xdf[[2]], outFile = "btree.xdf",
## overwrite = TRUE, cp = 0.01, nTree = 50, mTry = 3, seed = 123,
## lossFunction = "bernoulli")
##
##
## Loss function of boosted trees: bernoulli
## Number of boosting iterations: 50
## No. of variables tried at each split: 3
##
## OOB estimate of deviance: 1.273342
Compute predictions for evaluation
Lets see how the models performed using the famous ROC curve. Before we
do that, we need to compute the predicted values. We use the rxPredict
function on the our test data to predict the values. Then we will merge
all the predictions using the below chunk.
# Out data for prediction
logit_pred.xdf <- "logit_pred.xdf"
# Predict and write from Logit model
rxPredict(logit_model, data = train.test.xdf[[1]],
outData = logit_pred.xdf,
overwrite = TRUE,
writeModelVars = FALSE,
predVarNames = "logit_prob",
extraVarsToWrite = c("new_id", "bin_gender"))
# Predict and write from DForest model
forest_pred.xdf <- "forest_pred.xdf"
rxPredict(forest_model, data = train.test.xdf[[1]],
outData = forest_pred.xdf,
overwrite = TRUE,
type = "prob",
writeModelVars = FALSE,
predVarNames = c("forest_prob_F", "forest_prob_M", "gender_pred"),
extraVarsToWrite = c("new_id"))
# Predict and write from BTree model
btree_pred.xdf <- "btree_pred.xdf"
rxPredict(btree_model, data = train.test.xdf[[1]],
outData = btree_pred.xdf,
overwrite = TRUE,
writeModelVars = FALSE,
predVarNames = "btree_prob",
extraVarsToWrite = c("new_id"))
#Check the initial few records
i <- rxGetInfo(logit_pred.xdf, getVarInfo = TRUE, numRows = 5)
i$data
## logit_prob new_id bin_gender
## 1 0.7180527 16 0
## 2 0.7370044 51 0
## 3 0.6288687 64 1
## 4 0.5910179 285 0
## 5 0.6143816 363 1
# Merging all predictions
allpredictions.xdf <- "allpredictions.xdf"
allpredictions.xdf <- rxMerge(logit_pred.xdf, forest_pred.xdf,
matchVars = "new_id",
outFile = allpredictions.xdf,
type = "inner",
varsToDrop2 = c("forest_prob_F", "gender_pred"),
overwrite = TRUE
)
allpredictions.xdf <- rxMerge(allpredictions.xdf, btree_pred.xdf,
matchVars = "new_id",
outFile = allpredictions.xdf,
type = "inner",
overwrite = TRUE
)
i <- rxGetInfo(allpredictions.xdf, getVarInfo = TRUE, numRows = 5)
i$data
## logit_prob new_id bin_gender forest_prob_M btree_prob
## 1 0.7180527 16 0 0.6842109 0.6641452
## 2 0.7370044 51 0 0.6319882 0.6339701
## 3 0.6288687 64 1 0.6111347 0.6439666
## 4 0.5910179 285 0 0.5804147 0.6339701
## 5 0.6143816 363 1 0.6010502 0.6339701
Now that we have prediction probabilities from all 3 models lets visualize using an ROC curve.
Plotting the ROC Curve
We will use rxRoc function to compute the Sensitivity and Specificity
for the ROC curve.
rocOut <- rxRoc(actualVarName = "bin_gender",
predVarNames = c("logit_prob", "forest_prob_M", "btree_prob"),
data = allpredictions.xdf)
plot(rocOut)
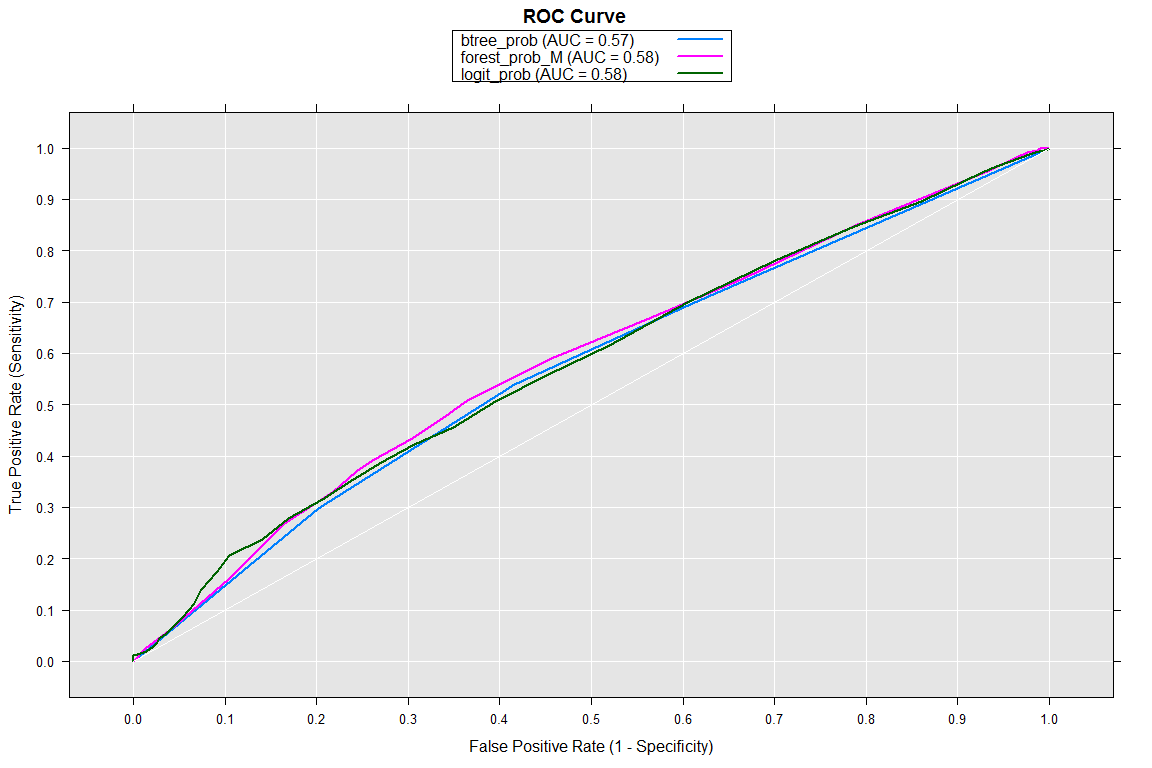
As per the area under the ROC curve we can select either the logistic regression or the decision forest as the best model. Please note that there is huge scope to further improve and tune the performance of these models which we are not covering in this post.
Conclusion
In this and the earlier post we have extensively used the RevoScaleR function to cover the entire gamut of machine learning experiement. Specifically we have seen:
-
Reading big data file in to
xdffiles -
Performaning exploratory data analysis and statistical test
-
Visualizing the data
-
Splitting the data in to train and validation sets
-
Building models
-
Evaluating the models
The RevoscaleR functions stand out particularly when working with large data files that do not fit in the memory. These powerful parallel and distributed functions work seamlessly in conjunction with Base R functions therefore alleviating the traditional challenges of R relating to scalability and performance.
Hope you liked this post. Please comment below for any query.